Booleaanse logica
Op basis van het voorgaande is duidelijk dat het mogelijk is om alle denkbare getallen om te zetten naar bits en dat onze normale rekenregels ook gelden voor deze binaire getallen. En met in het achterhoofd dat 0 gelijk staat aan geen spanning en 1 aan wel spanning, kun je dan ook beredeneren dat een processor in feite kan rekenen door op verschillende plekken wel of geen stroompjes te laten lopen. Maar hoe gaat dat dan in zijn werk met die honderden miljoenen schakelaars? Om dat te begrijpen, maken we een zijstap naar het fenomeen Booleaanse logica, de basis van hoe computers hun werk doen, uitgedacht door George Boole halverwege de 19de eeuw. Hij definieerde een systeem van logische poortjes die werken met 0’en en 1én, gates ofwel poorten in jargon, die je uiteindelijk aan elkaar kunt knopen om zo complexe bewerkingen met 0’en en 1’en uit te voeren. Al deze gates hebben één of twee ingangen en één uitgang. Je vindt de zogenaamde basispoorten in onderstaande afbeelding, met daar onder een schemaatje met alle mogelijke combinaties van de ingangen en de bijbehorende uitkomst.
De ingangen worden A en B genoemd. Om verwarring met het getal 0 te voorkomen, bedacht Bool dat de uitgang niet de O van output maar de letter Q moest krijgen. Er zijn drie basispoorten en vier aanvullende, die met de basispoorten gemaakt kunnen worden. Met in totaal zeven gates kunnen de meest complexe logische schakelingen gemaakt worden.

De 7 basis Booleaanse gates
Poorten
De eerste poort is de meeste simpele: de NOT (NIET) gate ook wel inverter genoemd, zet op zijn uitgang het tegenovergestelde van de ingang. Ofwel: als ingang A = 0 dan uitgang Q = 1 en als A = 1 dan Q = 0. De tweede gate is AND (EN) en heeft twee ingangen. Als beide ingangen 1 zijn, dan is de uitgang ook 1. Om het helemaal correct te formuleren: “Als A = 1 EN B = 1 dan Q = 1”. Als minimaal één van de ingangen 0 is, dan blijft de ingang ook 0. De derde basispoort is de OR (OF) gate: hier is de uitgang 1 als één van beide of allebei de ingangen 1 is. Om het weer correct te formuleren: “Als A = 1 OF B = 1 (of beide) dan Q = 1”.
Naast deze drie basis gates is er nog een viertal afgeleiden die in de Booleaanse logica veel gebruikt worden. Allereerst zie je de NOR en NAND Gates, afkortingen voor NOT OR (NIET OF) en NOT AND (NIET EN). Dit zijn in feite de OR and AND gates, maar dan met een inverter er achter. Ze hebben dus exact de tegenovergestelde uitkomst als OR and AND. Dat zie je ook duidelijk terug in de schemaatjes.
Ten slotte bevat het overzicht nog de XOR and XNOR, wat staat voor eXclusive OR (exclusieve OF) en eXclusive NOT OR (exclusieve NIET OF). Een XOR gate geeft 1 op z’n uitgang als A = 1 of B = 1, maar niet allebei. Een XNOR is doet exact het tegenovergestelde.
We schreven al dat de vier aanvullende poorten zijn te maken met een aaneenschakeling van de drie basis gates. Een XOR-gate is eenvoudig te bewerkstelligen door twee NOT’s, twee AND’s en een OR op elkaar aan te sluiten, zoals hieronder te zien. Reken de aaneenschakeling maar eens door, je ziet dat de uitkomst van Q exact overeenkomt met het schema van de XOR-gate. Laten we een als voorbeeld A = 1 en B = 0 nemen. De bovenste AND gate geeft dan 1 en 1 als ingang, de uitgang van deze AND is dan 1. De onderste AND gate heeft 0 en 0 als ingang, met dus ook 0 als uitgang. De OR gate aan het eind krijgt 1 en 0 binnen, wat resulteert in een 1. Je zult ziet dan alle andere ingangscombinatie ook exact het gedrag van een XOR opleveren.
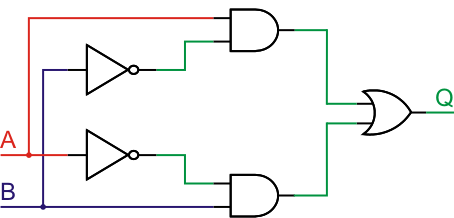
Een XOR-gate kun je maten met twee NOT’s, twee AND’s en één OR.










