Transistors
We hebben gezien dat de NAND en NOR gates in feite te maken zijn door een AND of OR en een NOT achter elkaar te plakken en ook de XOR en XNOR gates zijn te fabriceren vanuit NOT’s, AND’s en OR’s. Dat reduceert het aantal gates dat daadwerkelijk fysiek gefabriceerd moet worden tot drie.
Terug naar onze vrienden de transistors, die we uitgebreid in het vorige artikelhebben besproken. De transistor is zoals we beschreven een elektronisch component met drie aansluitingen (gate, source en drain), die werkt als een schakelaar. We schreven al dat ze het best te vergelijken zijn met een deurbel: zet je een spanning (een 1 dus!) op de gate, dan ontstaat er een verbinding tussen drain en source.
Het maken van de drie basis gates met transistors is met de deurbel in het achterhoofd niet ingewikkeld meer, zoals te zien in onderstaande afbeelding. Een AND gate maak je simpelweg door twee transistors achter elkaar te plaatsen. Alleen als bij beide transistors op de gate een spanning staat, komt de uitgang in verbinding met de hoofdspanning. Een OR gate maak je juist door twee transistors naast elkaar, ofwel parallel te plaatsen. Als bij minstens één van beide transistors een spanning op de gate staat, komt die ook op de uitgang. De inverter tenslotte is simpel te maken met één transistor en een weerstand.
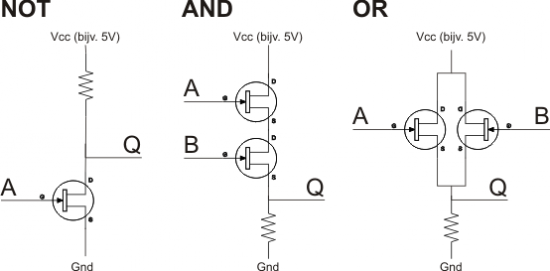
De drie basis gates uitgevoerd met transistors.
Adder
We hebben gezien dat je met nullen en enen kunt rekenen, we hebben de logische gates bekeken en aangetoond dat je de basis gates eenvoudig met één of twee transistors kunt fabriceren. Laten we tenslotte alles eens bij elkaar brengen: als je met een aaneenschakeling van logische gates berekeningen kan uitvoeren, kan dat dus ook met een aaneenschakeling van transistors. Wat zal blijken: ons voorbeeldje van hoe je binaire getallen kunt optellen, is relatief eenvoudig met logische gates te bewerkstelligen.
Laten we eens beginnen met een simpel schema dat twee bits bij elkaar moet optellen, in jargon een single-bit adder (to add is immers Engels voor optellen, een adder is dus een ‘opteller’). We hebben gezien dat er vier verschillende mogelijkheden zijn: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1 en 1 + 1 = 10. Onze single-bit adder moet dus twee uitgangen hebben; één voor de basis uitkomst en één om een eventuele bit over te hevelen, de carry-out in jargon. In afbeelding 6 zie je het complete schema met alle combinaties van de twee ingangen en de bijbehorende uitgangen Q en CO (carry-out). Wat blijkt: de Q uitgang komt exact overeen met de XOR-gate en de CO met de AND-gate! Het maken van een single-bit adder is dus een kwestie van twee logische gates gebruiken. Dat zie je dus ook in onderstaande afbeelding: in het diagram voeren we beide ingangen A en B naar zowel een XOR als een AND, met beide gewenste uitgangen als resultaat.
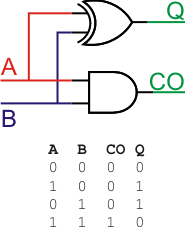
Met een XOR en een AND gate heb je al een single-bit adder.










