De zes stappen van het 3D rendering proces
Om te begrijpen wat er nu zo revolutionair is aan de nieuwe GeForce 256 moeten we eerst het hele proces van 3D rendering nog een keer bekijken.
In principe bestaat het creëren van 3D graphics in spellen als Quake en Unreal uit zes fases: een gedeelte van deze fases neemt de CPU voor zijn rekening, het andere gedeelte doet de videokaart. We zullen de zes fases binnen dit proces (waarvan overigens de vier laatste echt interessant zijn) eerst grondig analyseren. Huidige videokaarten nemen alleen de laatste twee stappen voor hun rekening: de eerste vier zijn nog altijd werk voor de CPU. Nieuw bij de GeForce 256 is dat stap 3 (Transformation) en stap 4 (Lightning) ook door de 3D-chip gebeuren. Aangezien de chip hier speciaal voor ontwikkeld is, kunnen deze fases sneller doorlopen worden en zal het gehele render proces een grote versnelling krijgen. Bijkomend voordeel is dat de CPU zo ook meer tijd over houdt voor andere zaken.
Fase 1 en 2: Applicatie specifieke taken en Scène Berekeningen
De eerste twee fases zijn duidelijk bestemd voor de CPU. De eerste fase bestaat uit een aantal applicatie specifieke zaken, zoals het berekenen van de plaats van alle objecten in de 3D wereld, het berekenen van het camerastandpunt etc. De tweede fase is ook duidelijk CPU gericht: hierin worden alle specifieke zaken voor een 3D scène berekend: welke objecten zijn wel of niet zichtbaar, welk detail is noodzakelijk voor welke objecten, etc.
Fase 3: Transformation
Pas nu bij fase drie komen we bij het echte render-werk uit. In de "Transformation" fase wordt het coördinaten stelsel van de 3D wereld omgerekend naar een coördinaten stelsel loodrecht op het beeldscherm. Dit is duidelijk te zien in de volgende afbeelding. We zien Woody (bekend van Toy Story) hier in het (x, y, z) coördinaten stelsel van de 3D game staan. Het grijze vlakje is de positie van het beeldscherm en dus van de toeschouwer. Het (x, y, z) stelsel zal omgerekend moeten worden naar een (x', y', z') stelsel waarvan twee assen gelijk zijn aan de assen van het scherm en waarvan de derde as loodrecht hierop staat.
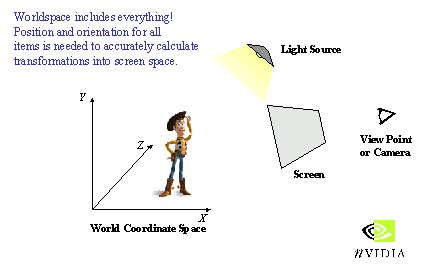
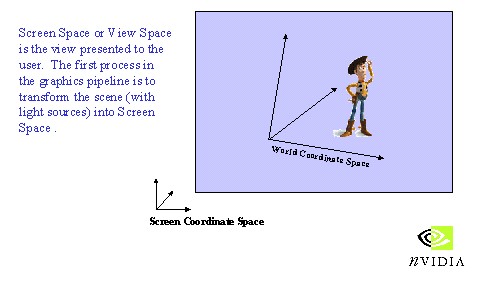
In onderstaande afbeelding is dit omreken proces duidelijk te zien. De positie van Woody is omgerekend naar een relatieve positie gezien vanuit het scherm. Duidelijk is het World Coördinaten Stelsel (x, y, z) en het Scherm Coördinaten Stelsel (x', y', z') te zien.
Personen met enige inzicht in Lineaire Algebra weten dat het omrekenen van coördinaten stelsel op niets anders neerkomt dat het uitvoeren van een matrix vermenigvuldiging. Onderstaande figuur toont deze wiskundige berekening. I.p.v. alleen een x, y en z is er in de praktijk ook nog een w nodig. Deze w is de zogenaamde schaling-factor voor de perspectief correctie. Om de (x, y, z, w) vector nu om te rekenen naar de nieuwe (x', y', z', w') vector is een bepaalde transformatiematrix benodigd. Deze transformatie vector is natuurlijk voor alle berekeningen binnen één 3D scène (binnen één frame dus) hetzelfde.
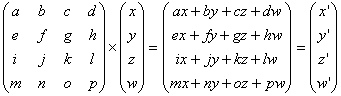
Duidelijk is dat voor het omrekenen van 1 punt maarliefst 16 vermenigvuldigingen en 12 optellingen nodig zijn. Voor iedere driehoek (triangle) binnen de 3D scène zijn er weer 3 omzettingen nodig (voor de drie hoekpunten). Al met al vergt deze transformatie fase dus heel wat rekenwerk. Hoewel CPU's door toevoegingen als MMX in het verleden al steeds geschikter zijn gemaakt voor deze matrix vermenigvuldigingen, blijft dit toch zeer veel (en omslachtig) werk voor de CPU. Een speciaal hiervoor gemaakte transformation-unit op de videokaart kan deze berekeningen veel sneller en efficiënter uitvoeren en ontlast daarmee ook de CPU.










